RC Circuit Behavior: Understand Natural Response

Demonstrative Video

RC Circuit without Source

Transients

  • We will study circuits that contain sources, switches, resistances, inductances, and capacitances.

  • The time-varying currents and voltages resulting from the sudden application of sources, usually due to switching, are called transients.

  • In transient analysis, we start by writing circuit equations using developed concepts, such as KCL, KVL, node-voltage analysis, and mesh-current analysis.

  • The \(I-V\) relationships for inductances and capacitances involve integrals and derivatives, we obtain integro-differential equations.

  • These equations can be converted to pure differential equations by differentiating with respect to time.

  • Thus, the study of transients requires us to solve differential equations.

First Order Circuits

  • A first-order circuit can only contain one energy storage element (a capacitor or an inductor).

  • The circuit will also contain resistance.

  • So there are two types of first-order circuits:

    1. RC circuit

    2. RL circuit

  • The first-order circuits are characterized by first-order differential equation.

Excitation of the Circuit

  • There are two ways to excite the circuits.

  • Source-free or Natural Response:

    • Initial conditions of the storage elements i.e. energy initially stored in the capacitive or inductive element.

    • The energy causes current to flow in the circuit and is gradually dissipated in the resistors.

    • Although source-free circuits are by definition free of independent sources, they may have dependent sources.

  • Forced Response:

    • Excitation by independent sources.

    • Sources: DC, sinusoidal, exponential

  • The two types of first-order circuits and the two ways of exciting them add up to the four possible situations.

The Source-Free RC Circuit

  • A source-free RC circuit occurs when its dc source is suddenly disconnected.

  • Energy stored in capacitor is released to resistors.

  • \(C\) and \(R\) may come as \(C_{eq}\) and \(R_{eq}\) from a complex circuit.

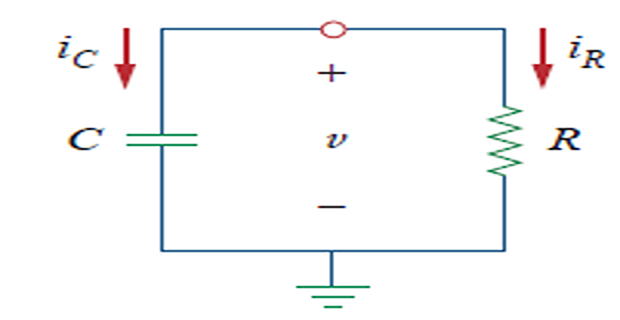
image

Natural response of RC circuit

\[\begin{aligned} &\text{Initial condition}~v(0)=V_{0} \\ &\text{Initial energy}~w(0)=\frac{1}{2} C V_{0}^{2} \\ &\text{KCL}~~i_{C}+i_{R}=0 \\ &\Rightarrow~C \frac{d v}{d t}+\frac{v}{R}=0 \\ &\Rightarrow~\frac{d v}{d t}+\frac{v}{R C}=0 \\ &\Rightarrow~\frac{d v}{v}=-\frac{1}{R C} d t \\ &\Rightarrow~\ln (v)=-\frac{t}{R C}+\ln (A) \\ &\Rightarrow~\ln \left(\frac{v}{A}\right)=-\frac{t}{R C} \\ &\Rightarrow~v(t)=A \cdot e^{-t / R C} \end{aligned}\]

  • voltage response of the RC circuit is an exponential decay of the initial voltage.

  • At \(t=0~\Rightarrow~v(t)=V_0\)

  • As \(t~\uparrow\) \(v~\downarrow\) to zero.

  • The rapidity with which the voltage decreases is expressed in terms of the time constant (\(\tau\))

  • Time constant: Time required for the response to decay to a factor of 1/e or 36.8% of its initial value.

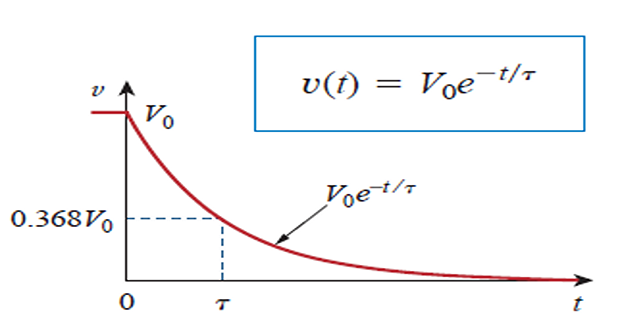
image
  • \[V_{0} e^{-\tau / R C}=V_{0} e^{-1}=0.368 V_{0}\]
    At

  • Therefore, \(\boxed{\tau = RC}\)

  • \[\boxed{v(t)=V_{0} e^{-t / \tau}}\]
    Hence,
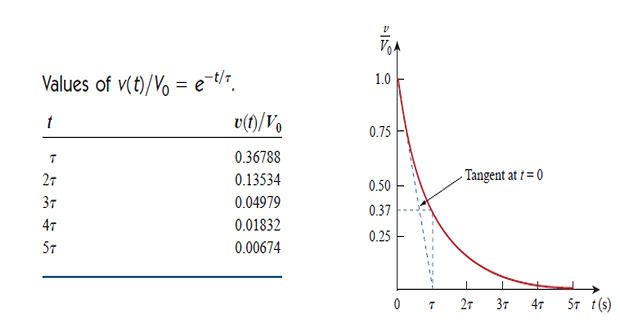
image

  • Note: \(v(t)\) is less than 1% of \(V_0\) after \(5\tau\)

  • Thus, it is customary to assume that the capacitor is fully discharged (or charged) after \(5\tau\).

  • In other words, it takes \(5\tau\) for the circuit to reach its final or steady state.

  • For every \(\tau\) time interval, \(v\) is reduced by 36.8% of its previous value.

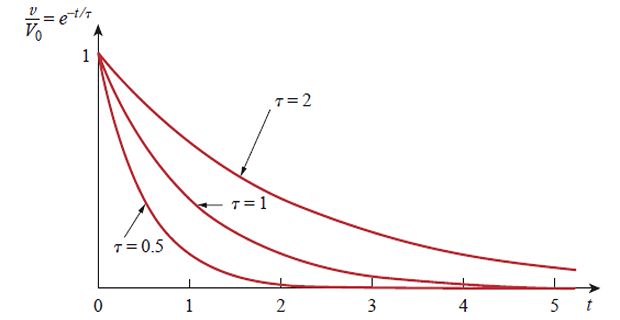
image

  • Smaller the \(\tau\), the more rapidly the voltage decreases, i.e., the faster the response to reach steady-state.

  • It reaches the steady state (or final state) quickly due to quick dissipation of energy stored.

\[\begin{aligned} i_{R}(t) &=\frac{v(t)}{R}=\frac{V_{0}}{R} e^{-t / \tau} \\ p(t) &=v i_{R}=\frac{V_{0}^{2}}{R} e^{-2 t / \tau} \\ w_{R}(t) &=\int_{0}^{t} p d t=\int_{0}^{t} \frac{V_{0}^{2}}{R} e^{-2 t / \tau} d t \\ &=-\left.\frac{\tau V_{0}^{2}}{2 R} e^{-2 t / \tau}\right|_{0} ^{t}=\frac{1}{2} C V_{0}^{2}\left(1-e^{-2 t / \tau}\right), \quad \tau=R C \end{aligned}\]

  • Notice that as \(t \rightarrow \infty, w_{R}(\infty) \rightarrow \frac{1}{2} C V_{0}^{2}\), which is the same as \(w_{C}(0)\) the energy initially stored in the capacitor.

  • The energy that was initially stored in the capacitor is eventually dissipated in the resistor.

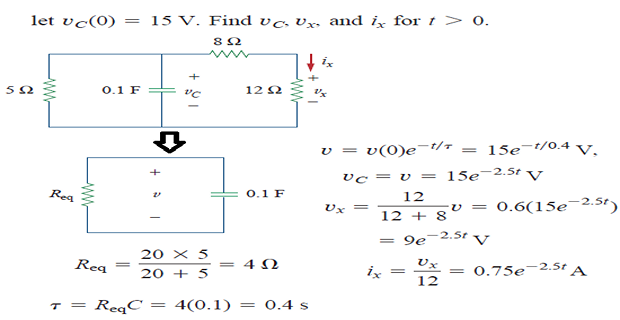
Problem Solving Steps

  • Determine capacitor initial voltage \(v(0)=V_0\)

  • Determine the time constant, \(\tau\)

  • Determine \(v_c(t)=v(t)=v(0)e^{-t/\tau}\)

  • Once \(v_c(t)\) is determined, then other variables \(i_c\), \(v_R\), and \(i_R\) can be easily solved

  • In finding, \(\tau=RC\), \(R=R_{TH}~\Rightarrow\) Thevenin equivalent resistance at the terminals of the capacitor; i.e. we take out \(C\) and find \(R=R_{TH}\) at its terminals.

Solved Problem

image